Symmetric Matrix Product Of Eigenvalues

LetAbe a symmetric matrix. Eigenvectors for a real symmetric matrix which belong to difierent eigen-values are necessarily perpendicular.

The Number Of Positive Eigenvalues Of A Non Singular Symmetric Matrix Is Equal To The Number Of Positive Pivots Strang Mathematics Stack Exchange

Enter your answers from smallest to largest - 3 4 0 0 4 -3 0 0 0 0 -3 4 0 0 4 -3 λι For each eigenvalue find the dimension of the corresponding eigenspace.

Symmetric matrix product of eigenvalues. 52 Quadratic Forms motivating quote from David Lays Third Ed Linear Algebra and Its Applica-tions. This fact has important consequences. The matrixUis called anorthogonal matrixifUTUIThis implies thatU UTI by uniqueness of inverses.

1 If you notice the matrix is symmetrical we can try to come up with an eigenvalue that can make the diagonal to all 0s. Let Aai li j. Since and are arbitrary eigenvectors for with distinct eigenvalues and they were shown to be orthogonal we can conclude in general that any pair of eigenvectors for with distinct eigenvalues will be orthogonal.

It follows that if 1. Any symmetric or skew-symmetric matrix for example is normal. I have seen the theorem that the product cannot have negative eigenvalues but I struggle to find an example of zero eigenvalue case.

The trace is equal to the sum of eigenvalues. I am trying to come up with an example but I always got positive definite matrices as a result. And since is an arbitrary real symmetric matrix as well we can conclude that for any real symmetric matrix any pair of eigenvectors with distinct eigenvalues will be orthogonal as desired.

Eigenvalues and Eigenvectors of Asymmetric Matrices. Then 1A maxxTAx kxk21. Symmetric Hermitianindefintematrix is one that has some positive andsome negative and possibly zero eigenvalues.

Negative definite Hermitian symmetric matrix must have all strictly neg-ative eigenvalues. However this last fact can be proved in an elementary way as follows. Assume flrst that the eigenvalues of A are distinct and that it is real and symmetric.

Read It -12 Points DETAILS LARLINALG8 73016. LetAbe a real symmetric matrix of sizeddand letIdenote theddidentity matrix. Let A and B be two real symmetric matrices one of which is positive definite.

Show that there is an n times n real matrix B such that B2A. Trave symmetric matrix then all its eigen vectors I4 A is a or tho. Therefore by the previous proposition all the eigenvalues of a real symmetric matrix are real.

If is a square but asymmetric real matrix the eigenvector-eigenvalue situation becomes quite different from the symmetric case. Then not only is there a basis consisting of eigenvectors but the basis elements are also mutually perpendicular. Let u 1 u n be the linearly independent eigenvectors which correspond to the positive eigenvalues λ 1 λ n of the real symmetric matrix A.

So it too is invertible. Nare the eigenvalues of A with corresponding orthonormal eigenvectors q 1q 2q n then we have AQ QD. Let rr4A be the eigenvalues.

The Rayleigh coecient gives a characterization of all eigenvalues andeigenvectors ofA in terms of the solution to optimization problems. The eigenvalues of a real skew-symmetric matrix are purely imaginary see below and to every eigenvalue there corresponds the conjugate eigenvalue with the same multiplicity. All the eigenvalues of a symmetric real matrix are real If a real matrix is symmetric ie then it is also Hermitian ie because complex conjugation leaves real numbers unaffected.

Perhaps themost important and useful property of symmetric matrices is that their eigenvalues behave very nicely. Let1 2 nbe theeigenvalues ofA. Q q 1 q n.

Left beginarrayccc 0 0 1 0 0 0 1 0 0 endarray right. So we can try eigenvalue 1 which makes the new matrix into. Solution for If a real matrix then the eigenvalues of AAT A is Ceal always are false.

Then it is easy to see that the product A B or B A which has the same eigenvalues is similar to a symmetric matrix so has real eigenvalues. Take the vectors of eigenvalues of A and of B sorted in decreasing order and let their componentwise product be a b. A Square Root Matrix of a Symmetric Matrix with Non-Negative Eigenvalues Let A be an ntimes n real symmetric matrix whose eigenvalues are all non-negative real numbers.

Furthermore the a with i i are required to have the same distribution function 4 while all the ú7í possess the same distribution G. Find the eigenvalues of the symmetric matrix. Enter your answers as a comma-separated list.

It can be shown that in this case the normalized eigenvectors of Aform an orthonormal basis for Rn. Also let z c 1 u 1 c n u n be a random n 1 real vector with z 0. In mathematics a self-adjoint operator on a finite-dimensional complex vector space V with inner product equivalently a Hermitian operator in the finite-dimensional case is a linear map A from V to itself that is its own adjoint.

For all vectors v and w. Therefore as the determinant is the product of the eigenvalues each one repeated according to its multiplicity it follows at once that the determinant if it. We gave a variational treatment of the symmetric case using the connection between eigenvalue problems and quadratic forms or ellipses and other conic sections if you have a geometric mindThat connection.

This is a sketch of a proof when the symmetric matrix A is real. 2 days agoLet us say A and B are symmetric positive definite matrices. Use the fact that a real symmetric matrix is diagonalizable by a real orthogonal matrix.

Can their product AB have all zero eigenvalues. If V is finite-dimensional with a given orthonormal basis this is equivalent to the condition that the matrix of A is a.

Eigenvalue Feature 4 The Trace Youtube

Eigenvalues And Eigenvectors Of Symmetric Matrices Linear Algebra

How To Find The Eigenvalues And Eigenvector For The Matrix M 3 4 1 1 Quora

How To Find The Third Eigenvector Of A 3x3 Matrix Given The Other Two Eigenvectors Mathematics Stack Exchange

Symmetric Matrix Decomposition With Orthonormal Basis Of Non Eigenvectors Mathematics Stack Exchange

Determinant Trace And Eigenvalues Of A Matrix Problems In Mathematics

Linear Algebra 101 Part 7 Eigendecomposition When Symmetric By Sho Nakagome Sho Jp Medium

Linear Algebra Matrix Eigen Value Problems Ppt Download

Eigenvalues And Eigenvectors

Http Www Cse Iitm Ac In Vplab Courses Larp 2018 Chap5 Evv Larp Pdf

Eigenvalues Of A Matrix And Its Transpose Are The Same Problems In Mathematics

Eigenvalues Eigenvectors 7 1 Eigenvalues Eigenvectors N N

Symmetric Matrices Eigenvalues Eigenvectors Youtube

Eigenvalues And Eigenvectors Of Symmetric Matrices Linear Algebra

What Are The General Form Of Eigenvalues Of An Orthogonal Matrix Mathematics Stack Exchange

Linear Algebra Example Problems Eigenvalue Computation 3 Youtube

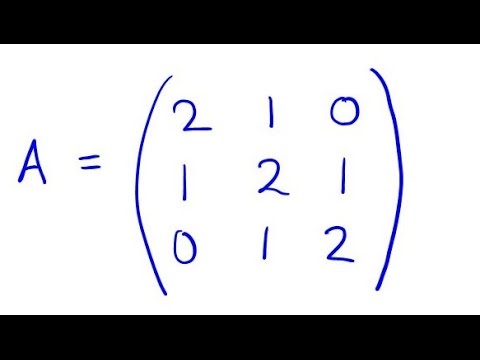
Find Eigenvalues Of 3x3 Matrix Youtube

Eigenvalue Of Matrix Determinant Equals To The Product Of All Its Eigenvalue Mathematics Stack Exchange

Karl Stratos Research Eigentutorial