Matrix Sum Of Symmetric And Antisymmetric
But if it can be done along the lines I tried with indexes Id really like to see that - I am looking for opportunities to practice Indexing. 6 Any square matrix can be expressed as the sum of symmetric and antisymmetric parts.

Symmetric And Skew Symmetric Matrices Definition Theorem Solved Example Problems
U i j k.

Matrix sum of symmetric and antisymmetric. A matrix is symmetric if for each pair of indices i and j the i j entry equals. Today we prove that. So A A is a skew symmetric matrix Now Lets write matrix A as sum of symmetric skew symmetric matrix A A A A 2A So 12 A A A A A 12 A A 12 A A A Here 12 A A is the symmetric matrix 12 A A is the symmetric matrix.
From the Theorem 1 we know that A A is a symmetric matrix and A A is a skew-symmetric matrix. Let MS be a symmetric and negative definite matrix and MA be an anti-symmetric matrix both in R. Furthermore once the matrix product is known then the second product can be replaced by its transpose.
Since for any matrix A kA kA it follows that 1 2 AA is a symmetric matrix and 1 2 A A is a skew-symmetric matrix. Let A be a square matrix then we can write A 12 A A 12 A A. The general antisymmetric matrix is of the form.
In component notation this becomes. Thanks Evgeny I used Tr AB T Tr A T B Tr A T BTr AB and Tr AB T Tr A -B-Tr AB So Tr AB-Tr AB therefore Tr AB0. Any matrix A can be written as a sum of its symmetric and antisymmetric parts ie ANA A where 1 4 4 and A.
The eigenvalues of MS lie in the negative part of the complex plane while the eigenvalues of MA are found on the imaginary axis. Iii 8331221452 Let A 8331221452 A 8324325112 12 A A 12 8331221452. As the term part suggests a tensor is the sum of its symmetric part and antisymmetric part for a given pair of indices as in U i j k.
Now P Q 12 A A 12 A A A Thus A is a sum of symmetric skew symmetric matrix Ex 33 10 Express the following matrices as the sum of a symmetric and a skew symmetric matrix. Where C is the square matrix that we want to decompose C T its transpose and finally S and A are the symmetric and antisymmetric matrices respectively into which matrix C is decomposed. Applying to both sides of the antisymmetry condition gives.
Feb 3 2015. The statement in this question is similar to a rule related to linear algebra and matrices. Eigenvalues of the sum of a symmetric and a anti-symmetric matrix.
A peculiarity that square matrices have is that they can be decomposed into the sum of a symmetric matrix plus an antisymmetric matrix. Using indicial notation show that the square matrix can be expressed as the sum of a symmetric and antisymmetric matrix by the decomposition. U i j k.
The commutator of a symmetric matrix with an antisymmetric matrix is always a symmetric matrix. The j i entry. Any Square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix.
Any square matrix can expressed or represented as the sum of symmetric. Letting the requirement becomes. A matrix is antisymmetric if each i j entry is the negative of the j i.
5 Applying to both sides of the antisymmetry condition gives. 4 so an antisymmetric matrix must have zeros on its diagonal. Any Square Matrix can be expressed as the sum of symmetric and antisymmetric parts.
So an antisymmetric matrix must have zeros on its diagonal. The general antisymmetric matrix is of the form. Im interested in bounds for the eigenvalues of M MS MA.
A Give a symmetric 22 matrix and an antisymmetric 22 matrix. The formula that allows us to do it is the following. The commutator of matrices of the same type both symmetric or both antisymmetric is an antisymmetric matrix.
In the last tensor video I mentioned second rank tensors can be expressed as a sum of a symmetric tensor and an antisymmetric tensor.

Example 22 Express Matrix B As Sum Of Symmetric And Skew

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric
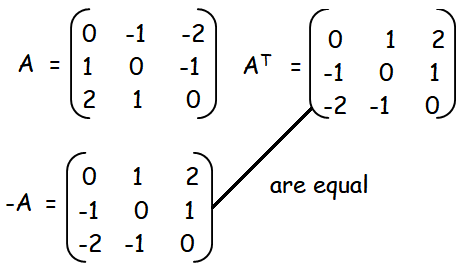
Questions On Symmetric And Skew Symmetric Matrix

5 Write The Following Matrix A As The Sum Of A Chegg Com

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric

Example 6 Express The Matrix A As The Sum Of A Symmetric And A Skew Symmetric Matrix Where Youtube

Example 22 Express Matrix B As Sum Of Symmetric And Skew

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric

Symmetric And Skew Symmetric Matrix Theorems Videos And Examples

Express The Following Matrix As The Sum Of A Symmetric And Skew
Express The Matrix As The Su Mathematics Topperlearning Com Cn7fu8s00
Express The Following Matrix As The Sum Of A Symmetric And A Skew Symmetric Matrix Mathematics Topperlearning Com Xeyte9b99
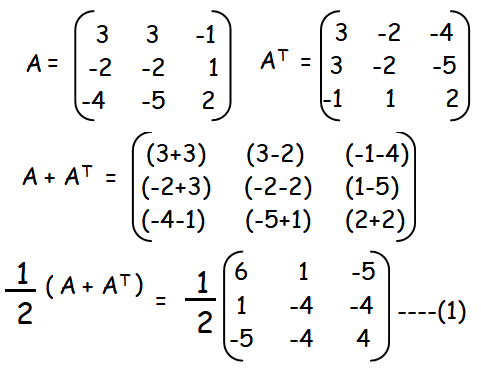
How To Express The Given Matrix As Sum Of Symmetric And Skew Symmetric

Example 22 Express Matrix B As Sum Of Symmetric And Skew

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric

Ex 3 3 10 Express As Sum Of A Symmetric A Skew Symmetric
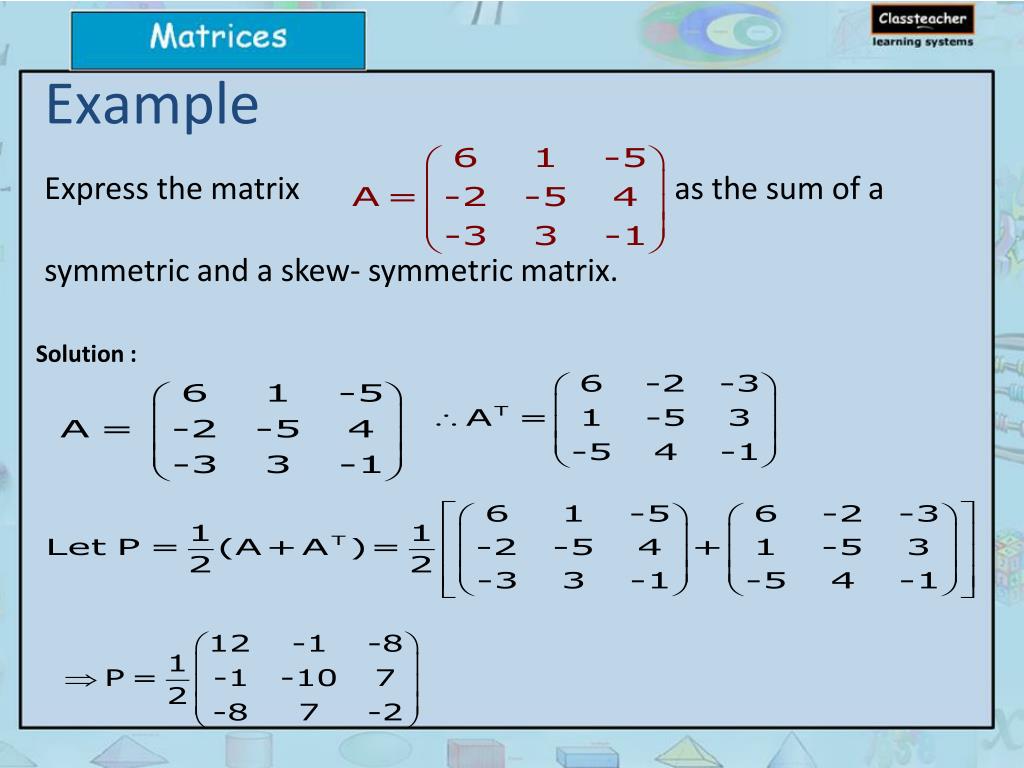
Ppt Symmetric And Skew Symmetric Matrices Powerpoint Presentation Free Download Id 2646318
Express The Following Matrix As The Sum Of A Symmetric And A Skew Symmetric Matrix Mathematics Topperlearning Com Xeyte9b99